IB
Free
- 2 students
- 78 lessons
- 0 quizzes
- 10 week duration
-
Topic 1: Number and algebra
- SL 1.1 Operations with numbers in the form a×10k where 1≤a<10 and k is an integer.
- SL1.2 Arithmetic sequences and series. Use of the formulae for the nth term and the sum of the first n terms of the sequence. Use of sigma notation for sums of arithmetic sequences.
- SL 1.3 Geometric sequences and series. Use of the formulae for the n th term and the sum of the first n terms of the sequence.
- SL 1.4 Financial applications of geometric sequences and series: • compound interest • annual depreciation.
- SL 1.5 Laws of exponents with integer exponents.
- SL 1.6 Simple deductive proof, numerical and algebraic; how to lay out a left-hand side to right-hand side (LHS to RHS) proof. The symbols and notation for equality and identity.
- SL 1.7 Laws of exponents with rational exponents.
- SL 1.8 Sum of infinite convergent geometric sequences.
- SL 1.9 The binomial theorem: expansion of (a+b)n,n∈ℕ.
- AHL 1.10 Counting principles, including permutations and combinations.
- AHL 1.11 Partial fractions.
- AHL 1.12 Complex numbers: the number i, where i2=−1. Cartesian form z=a+bi; the terms real part, imaginary part, conjugate, modulus and argument.
- AHL 1.13 Modulus–argument (polar) form: z=r(cosθ+isinθ)=rcisθ. Euler form: z=reiθ Sums, products and quotients in Cartesian, polar or Euler forms and their geometric interpretation.
- AHL 1.14 Complex conjugate roots of quadratic and polynomial equations with real coefficients.
-
AHL 1.15 Proof by mathematical induction.
Proof by contradiction.
Use of a counterexample to show that a statement is not always true. - AHL 1.16 Solutions of systems of linear equations (a maximum of three equations in three unknowns),including cases where there is a unique solution, an infinite number of solutions or no solution.
-
Topic 2: Functions
-
SL 2.1 Different forms of the equation of a straight line.
Gradient; intercepts.
Lines with gradients m1 and m2
Parallel lines m1=m2.
Perpendicular lines m1×m2=−1. -
SL 2.2 Concept of a function, domain, range and graph. Function notation, for example f(x), v(t), C(n). The concept of a function as a mathematical model.
Informal concept that an inverse function reverses or undoes the effect of a function. Inverse function as a reflection in the line y=x, and the notation f−1(x). -
SL 2.3 The graph of a function; its equation y=f(x).
Creating a sketch from information given or a context, including transferring a graph from screen to paper.
Using technology to graph functions including their sums and differences. -
SL 2.4 Determine key features of graphs.
Finding the point of intersection of two curves or lines using technology. -
SL 2.5 Composite functions.
Identity function. Finding the inverse function f−1(x). - SL 2.6 The quadratic function f(x)=ax2+bx+c: its graph, y -intercept (0,c). Axis of symmetry. The form f(x)=a(x−p)(x−q), x- intercepts (p,0) and (q,0). The form f(x)=a(x−h)2+k, vertex (h,k).
-
SL 2.7 Solution of quadratic equations and inequalities. The quadratic formula.
The discriminant Δ=b2−4ac and the nature of the roots, that is, two distinct real roots, two equal real roots, no real roots. -
SL 2.8 The reciprocal function f(x)=1/x,x≠0: its graph and self-inverse nature.
Rational functions of the form f(x)=(ax+b)/(cx+d) and their graphs. Equations of vertical and horizontal asymptotes. - SL 2.9 Exponential functions and their graphs: f(x)=ax, a>0, f(x)=ex Logarithmic functions and their graphs: f(x)=logax, x>0, f(x)=lnx, x>0.
-
SL 2.10 Solving equations, both graphically and analytically.
Use of technology to solve a variety of equations, including those where there is no appropriate analytic approach.
Applications of graphing skills and solving equations that relate to real-life situations. -
SL 2.11 Transformations of graphs.
Translations: y=f(x)+b;y=f(x−a).
Reflections (in both axes): y=−f(x);y=f(−x).
Vertical stretch with scale factor p: y=pf(x).
Horizontal stretch with scale factor 1/q: y=f(qx). -
AHL 2.12 Polynomial functions, their graphs and equations; zeros, roots and factors. The factor and remainder theorems.
Sum and product of the roots of polynomial equations. - AHL 2.13 Rational functions of the form f(x)=(ax+b)/(cx2+dx+e), and f(x)=(ax2+bx+c)/(dx+e)
-
AHL 2.14 Odd and even functions.
Finding the inverse function, f−1(x), including domain restriction.
Self-inverse functions. - AHL 2.15 Solutions of g(x)≥f(x), both graphically and analytically.
-
AHL 2.16 The graphs of the functions, y=|f(x)|
and
y=f(|x|), y=1/f(x), y=f(ax+b), y=[f(x)]2.
Solution of modulus equations and inequalities.
-
SL 2.1 Different forms of the equation of a straight line.
-
Topic 3: Geometry and trigonometry
-
SL 3.1 The distance between two points in three-dimensional space, and their midpoint.Volume and surface area of three-dimensional solids including right-pyramid, right cone, sphere, hemisphere and combinations of these solids.
The size of an angle between two intersecting lines or between a line and a plane. -
SL 3.2 Use of sine, cosine and tangent ratios to find the sides and angles of right-angled triangles.
The sine rule: a/sinA=b/sinB=c/sinC. The cosine rule: c2=a2+b2−2abcosC; cosC=a2+b2−c2/2ab .
Area of a triangle as 1/2absinC. -
SL 3.3 Applications of right and non-right angled trigonometry, including Pythagoras’s theorem. Angles of elevation and depression.
Construction of labelled diagrams from written statements. - SL 3.4 The circle: radian measure of angles; length of an arc; area of a sector.
-
SL 3.5 Definition of cosθ, sinθ in terms of the unit circle.
Definition of tanθ as sinθ/cosθ.
Exact values of trigonometric ratios of 0, π/6, π/4, π/3, π/2
and their multiples.
Extension of the sine rule to the ambiguous case. -
SL 3.6 The Pythagorean identity cos2θ+sin2θ=1. Double angle identities for sine and cosine.
The relationship between trigonometric ratios. -
SL 3.7 The circular functions sinx, cosx, and tanx; amplitude, their periodic nature, and their graphs Composite functions of the form f(x)=asin(b(x+c))+d.
Transformations.
Real-life contexts. -
SL 3.8 Solving trigonometric equations in a finite interval, both graphically and analytically.
Equations leading to quadratic equations in sinx,cosx or tanx. -
AHL 3.9 Definition of the reciprocal trigonometric ratios secθ, cosecθ and cotθ.
Pythagorean identities:1+tan2θ=sec2θ 1+cot2θ=cosec2θ -
AHL 3.10 Compound angle identities.
Double angle identity for tan. - AHL 3.11 Relationships between trigonometric functions and the symmetry properties of their graphs.
-
AHL 3.12 Concept of a vector; position vectors; displacement vectors. Representation of vectors using directed line segments. Base vectors i, j, k. Components of a vector:
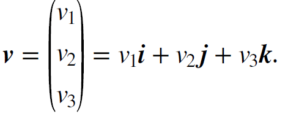
Algebraic and geometric approaches to the following:
• the sum and difference of two vectors
• the zero vector 0, the vector −v
• multiplication by a scalar, kv, parallel vectors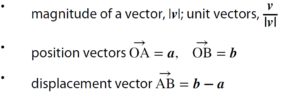
-
AHL 3.13 The definition of the scalar product of two vectors.
The angle between two vectors.
Perpendicular vectors; parallel vectors.
-
SL 3.1 The distance between two points in three-dimensional space, and their midpoint.Volume and surface area of three-dimensional solids including right-pyramid, right cone, sphere, hemisphere and combinations of these solids.
-
Topic 4: Statistics and probability
-
SL 4.1 Concepts of population, sample, random sample, discrete and continuous data.
Reliability of data sources and bias in sampling.
Interpretation of outliers.
Sampling techniques and their effectiveness. -
SL 4.2 Presentation of data (discrete and continuous): frequency distributions (tables).
Histograms.
Cumulative frequency; cumulative frequency graphs; use to find median, quartiles, percentiles, range and interquartile range (IQR).
Production and understanding of box and whisker diagrams. -
SL 4.3 Measures of central tendency (mean, median and mode).
Estimation of mean from grouped data.
Modal class.
Measures of dispersion (interquartile range, standard deviation and variance).
Effect of constant changes on the original data.
Quartiles of discrete data. -
SL 4.4 Linear correlation of bivariate data. Pearson’s product-moment correlation coefficient, r.
Scatter diagrams; lines of best fit, by eye, passing through the mean point.
Equation of the regression line of y on x.
Use of the equation of the regression line for prediction purposes. Interpret the meaning of the parameters, a and b, in a linear regression y=ax+b. -
SL 4.5 Concepts of trial, outcome, equally likely outcomes, relative frequency, sample space (U) and event. The probability of an event A is P(A)=n(A)/n(U).
The complementary events A and A′ (not A).
Expected number of occurrences. -
SL 4.6 Use of Venn diagrams, tree diagrams, sample space diagrams and tables of outcomes to calculate probabilities.
Combined events: P(A∪B)=P(A)+P(B)−P(A∩B). Mutually exclusive events: P(A∩B)=0.
Conditional probability: P(A|B)=P(A∩B)/P(B).
Independent events: P(A∩B)=P(A)P(B). - SL 4.7 Concept of discrete random variables and their probability distributions. Expected value (mean), for discrete data. Applications.
-
SL 4.8 Binomial distribution.
Mean and variance of the binomial distribution. -
SL 4.9 The normal distribution and curve. Properties of the normal distribution. Diagrammatic representation.
Normal probability calculations.
Inverse normal calculations -
SL 4.10 Equation of the regression line of x on y.
Use of the equation for prediction purposes. - SL 4.11 Formal definition and use of the formulae: P(A|B)=P(A∩B)/P(B) for conditional probabilities, and P(A|B)=P(A)=P(A|B′) for independent events.
-
SL 4.12 Standardization of normal variables (z- values).
Inverse normal calculations where mean and standard deviation are unknown. - AHL 4.13 Use of Bayes’ theorem for a maximum of three events.
-
AHL 4.14 Variance of a discrete random variable.
Continuous random variables and their probability density functions.
Mode and median of continuous random variables.
Mean, variance and standard deviation of both discrete and continuous random variables.
The effect of linear transformations of X.
-
SL 4.1 Concepts of population, sample, random sample, discrete and continuous data.
-
Topic 5: Calculus
-
SL 5.1 Introduction to the concept of a limit.
Derivative interpreted as gradient function and as rate of change. -
SL 5.2 Increasing and decreasing functions.
Graphical interpretation of f′(x)>0,f′(x)=0,f′(x)<0. -
SL 5.3 Derivative of f(x)=axn is f′(x)=anxn−1, n∈ℤ The derivative of functions of the form f(x)=axn+bxn−1….
where all exponents are integers. - SL 5.4 Tangents and normals at a given point, and their equations.
-
SL 5.5 Introduction to integration as anti-differentiation of functions of the form f(x)=axn+bxn−1+…., where n∈ℤ, n≠−1
Anti-differentiation with a boundary condition to determine the constant term.
Definite integrals using technology. Area of a region enclosed by a curve y=f(x) and the x -axis, where f(x)>0. -
SL 5.6 Derivative of xn(n∈ℚ), sinx, cosx, ex and lnx. Differentiation of a sum and a multiple of these functions.
The chain rule for composite functions.
The product and quotient rules. - SL 5.7 The second derivative. Graphical behaviour of functions, including the relationship between the graphs of f,f′ and f″.
-
SL 5.8 Local maximum and minimum points. Testing for maximum and minimum.
Optimization.
Points of inflexion with zero and non-zero gradients. - SL 5.9 Kinematic problems involving displacement s, velocity v, acceleration a and total distance travelled.
-
SL 5.10 Indefinite integral of xn(n∈ℚ),sinx,cosx,1/x and ex.
The composites of any of these with the linear function ax+b.
Integration by inspection (reverse chain rule) or by substitution for expressions of the form: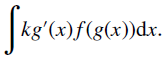
-
SL 5.11 Definite integrals, including analytical approach.
Areas of a region enclosed by a curve y=f(x) and the x-axis, where f(x) can be positive or negative, without the use of technology.
Areas between curves. -
AHL 5.12 Informal understanding of continuity and differentiability of a function at a point.
Understanding of limits (convergence and divergence). Definition of derivative from first principles.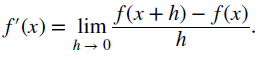
Higher derivatives. -
AHL 5.13
Repeated use of l’Hôpital’s rule. -
AHL 5.14 Implicit differentiation.
Related rates of change.
Optimisation problems. -
AHL 5.15 Derivatives of tanx, secx, cosecx, cotx, ax, logax, arcsinx, arccosx, arctanx.
Indefinite integrals of the derivatives of any of the above functions. The composites of any of these with a linear function.
Use of partial fractions to rearrange the integrand. -
AHL 5.16 Integration by substitution.
Integration by parts.
Repeated integration by parts. - AHL 5.17 Area of the region enclosed by a curve and the y-axis in a given interval. Volumes of revolution about the x-axis or y-axis.
-
AHL 5.18 First order differential equations. Numerical solution of dy/dx=f(x,y) using Euler’s method.
Variables separable.
Homogeneous differential equation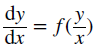
using the substitution y=vx.
Solution of y′+P(x)y=Q(x), using the integrating factor. -
AHL 5.19 Maclaurin series to obtain expansions for ex, sinx, cosx, ln(1+x), (1+x)p, p∈ℚ.
Use of simple substitution, products, integration and differentiation to obtain other series.
Maclaurin series developed from differential equations.
-
SL 5.1 Introduction to the concept of a limit.
0.00 average based on 0 ratings
5 Star
0%
4 Star
0%
3 Star
0%
2 Star
0%
1 Star
0%
Free